论文来源：https://doi.org/10.1145/3639283

问题背景

可控表格数据合成技术能够在多种场景下提供帮助，它使得用户可以根据自己设定的条件来生成数据。例如，用户可以指定生成的数据中某些字段的值必须符合特定的要求（预定义属性值），或者生成的数据需要与另一个已有的数据表（外部表）在某种特征上存在一定关联性。这种技术在数据保护、数据分析和机器学习等领域非常有用，因为它可以在不泄露真实数据隐私的情况下，帮助研究人员和开发人员获得所需的数据样本。而上述可控表格数据合成技术的功能可以总结为表内数据增强与表间数据增强两种形式的目的。

问题分析

对表格数据的分析

表格数据是一种数据组织形式，它将信息排列在表格中，表格由行（记录）和列（字段）组成。每一列通常对应数据的一个属性或特征，比如人的姓名、年龄、地址等。每一行则代表一个数据实例或记录，包含了所有列属性的具体值。这种数据结构非常常见，易于查询和分析，因此被广泛应用于数据库、电子表格、数据科学和商业智能等领域。下面给出的表格数据的一些共性，这些特性会影响之后可控表格数据合成技术的分析：

异质性：表格数据的异构性表现在其特征的多态性，涵盖了分类型、数值型、二元型以及文本型等不同特征类型。由此，特征的表现形式可以从密集的数值变量延伸至稀疏的或具有高类别数的分类变量。这意味着数据的生成需要考虑使用各种预处理技术，将不同数据通过归一化，合成或编码等手段进行处理，以提供给模型处理。
稀疏性：稀疏性现象在现实世界的应用场景中普遍存在，例如在临床试验、流行病学研究、欺诈检测等领域，频繁遭遇类别标签的不均衡分布以及数据值的缺失，进而引致训练样本集中呈现长尾分布的特征。这意味着数据的生成应该倾向于对少数样本进行补充以达到相对平衡的结果。
相关性：在表格数据的背景下，部分特征之间存在相关性。以人口统计数据为例，年龄、教育水平和酒精摄入量等因素相互交织：低龄群体获得博士学位的可能性较低，同时存在法定饮酒年龄下限。当回归模型纳入这些相关联的解释变量时，可能会导致估计系数的偏误。这意味着数据的生成需要对这些错综复杂的特征关系有所体现。
顺序不变性：数据集中的样本和特征排列顺序的改变不会影响数据的本质属性。与文本和图像数据不同，后者数据的解读强烈依赖于单词、标记或像素的相对位置，表格数据对于排列顺序的变化表现出较高的鲁棒性。这意味着那些依赖于位置信息的方法，如空间相关性分析、归纳偏置的引入以及卷积神经网络等，在处理表格数据时其效用相对较低¹。
先验知识较少：在图像和音频数据领域，通常存在关于数据的空间或时间架构的先验信息，这些信息可以在模型训练过程中被利用以提升学习效果。相反，对于表格数据，此类先验知识通常较为稀缺，这增加了模型识别和理解特征间内在联系的难度。这意味着表格数据的学习任务往往面临着更高的挑战，特别是在揭示数据潜在结构和关系方面 ²。

对当前表格数据生成方法的简述

以“ Tabular data generation model ”为关键词从谷歌学术上检索后，目前主流的表格数据生成方法主要基于以下几种方法：

GAN：利用生成对抗网络 GAN 给定生成器和判别器，生成器的目标是创造出尽可能接近真实数据分布的假数据，而判别器的任务是区分真实数据和生成器产生的假数据，而在 GAN 模型基础上控制生成数据的方法可以使用条件向量来指定要生成的特定特征值或类标注
ARM：通过学习数据序列的概率分布来有序且自回归直接生成新的数据，每个数据项的生成都是基于之前所有数据项的值，这意味着生成过程是有序的，并且每个数据项都依赖于之前的数据项。
Diffusion Model：处理后变成连续向量的表格数据可以被去噪概率扩散模型学习其分布，可以在生成过程中被条件引导，用于生成满足特定条件的合成数据。针对问题一的 RelDDPM 便属于该范畴。
VAE：用编码器将表格数据映射到潜在空间，学习数据的潜在表示，根据编码器输出的均值和方差，从标准正态分布中采样一个点，并通过重参数化技巧获得潜在空间的样本，然后使用解码器将潜在空间的样本映射回原始数据空间，得到重建的表格数据。

模型的建立

总体而言，问题一给出的 RelDDPM 方案可以概述为构建一个基于扩散模型的无条件生成模型和一个轻量级控制器来指导无条件生成模型生成满足不同条件的合成数据，具体示意图如下所示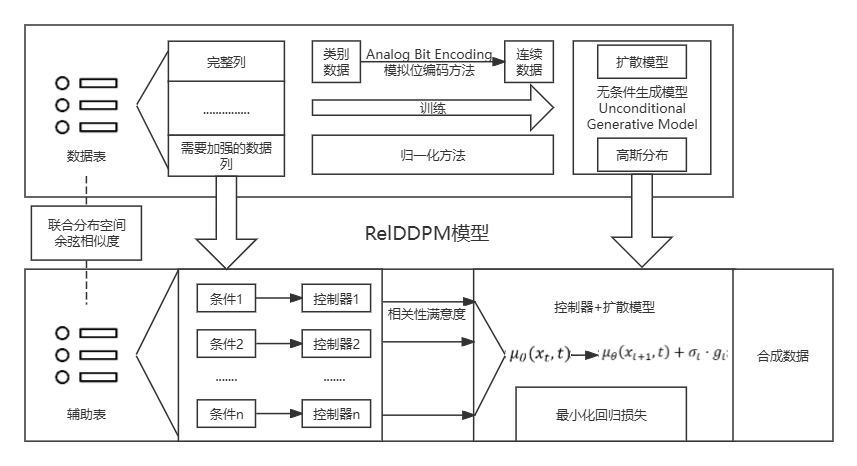： RelDDPM模型示意图

扩散模块的介绍

总体而言，扩散模块的核心就是 DDPM。去噪扩散概率模型（DDPM）是经过训练以逐渐去除噪声数据的参数化马尔可夫链。最初 DDPM 使用于高质量的图像生成，其存在一个前向过程和一个逆向过程，其前向过程用于向图像添加高斯噪声，而在逆向过程中则逐渐去除这个高斯噪声。

前向过程于给定的初始数据分布$x_0$ ~ $q(x)$，往其中逐步添加高斯噪声，持续 T 次，并产生一系列的噪声数据$x_1,…,x_T$，具体过程如下公式所示：

\[ q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\bar{\alpha}_t}x_0,(1-\bar{\alpha}_t)I) \]

其中，$q(x_t|x_{t-1})$ 表示在给定 $x_{t-1}$ 的条件下，$x_t$ 的概率分布，且在正向过程中，这个分布通常是高斯分布。同时，这里的$N$表示正态分布，$\sqrt{1-\beta_t}$ 是 $x_{t-1}$ 的系数，$β_t$是噪声比例参数并且在区间 $(0,1)$ 内，$I$ 是单位矩阵。接着，定义$ε_t$为从标准正态分布 $N (0, I) $中采样的噪声，于是我们可以改写上式为 $x_t = \sqrt{1 - \beta_t} \, x_{t-1} + \sqrt{\beta_t} \, \epsilon_t$，而在经过高斯函数叠加和重参数化的重复过程后，我们可以推导计算得到：

\[ q(x_t|x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t} x_0, (1 - \bar{\alpha}_t) I) \]

其中， $\alpha_t=1-\beta_t$ ，而 \[\bar{\alpha}_{t}=\prod_{t=1}^{T}\alpha_{t} \] 同时，当 $T\to\infty$ 时，$x_{T}$ 将成为一个具有高斯分布的噪声。
逆向过程逆向过程，即从$q(x_{t-1}\ |\ x_t)$中采样，就可以从一个随机的高斯分布$\mathcal{N} (0, I)$中逐渐去噪重建出一个真实的原始样本$x_0$，而$x_0$就是具有目标数据分布的合成数据。由于在前向过程中从前一时刻向后一时刻加入的是根据正态分布随机采样的噪声，因此从$x_t$到$x_{t-1}$也是一个难以预测的随机过程，但是可以通过贝叶斯公式大致地推测出给定$x_t$条件下$x_{t-1}$的概率分布：

\[ p_\theta(x_{t-1}\ |\ x_t)\ =\ \mathcal{N}(x_{t-1};\mu_\theta(x_t,t){,\left(\sqrt{\frac{\beta_t(1-{\bar{\alpha}}_{t-1})}{1-{\bar{\alpha}}_t}}\right)}^2) \]

其中，$\mu_\theta(x_t,t)$表示为模型预测的均值，${,\left(\sqrt{\frac{\beta_t(1-{\bar{\alpha}}_{t-1})}{1-{\bar{\alpha}}_t}}\right)}^2$是模型预测的标准差，而$\mu_\theta(x_t,t)$可以表示为：

\[ \mu_\theta(x_t,t)=\frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t}x_t+\frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t}\times\frac{x_t-\sqrt{1-\bar{a}_t}\times\varepsilon}{\sqrt{\bar{a}_t}}\cdot \]

其中，$ε$是从一个标准正态分布中 "随机抽取" 的噪声样本，只有找到与正向过程一致或接近的随机采样噪声值（噪声的概率分布已推测出）才能顺利产生合成样本，而$ε$由神经网络模型进行学习输出，在参考文献中使用最小化回归损失去更新的参数。

控制器模块的介绍

总体而言，控制器模块就是通过学习原始关系表中的属性分布和关联模式，来合成既符合真实数据特性又满足特定条件的新的数据记录。这个过程包括，先利用无条件扩散模型捕获整个数据表$R$的无条件分布$p(t)$，即不考虑任何额外条件下的属性值分布，然后基于给定的条件$C$，如特定的属性值范围或关联属性的条件，捕获条件分布$p(t|c)$，并利用控制器输出相关性满意度分数，以确保生成的每条记录不仅整体上看起来像是从原始表中抽取的，而且还要符合预定的条件，从而实现数据的可控合成。其中，条件$C$的来源可以分为以下两类：

表内条件：$C$是表$R$中的一组属性，它确保生成的元组满足$R$中指定属性的指定条件。
表间条件：$C$中的属性来自与表$R$存在主键-外键引用关系的外部表，旨在确保生成的数据在这两个相关表之间保持期望的相关性。同时，对于控制器而言，其目标是生成一个相关性满意度分数的方案$Ctrl(t^{\prime},c)$，这意味着生成的元组$t^{\prime}$应该尽可能地与条件实例$c$相关。因此参考文献使用了利用两个编码器（分别编码生成的元组和条件实例）进行对比学习捕捉数据关键特征，并利用余弦相似度计算相似度。

控制器模块的技术原理

首先对于条件$C$而言，不管表内表间，就其目的，即捕获对应的条件概率分布$p(t|c)$去从学习分布中采样合成元组，其本质都可以视作一个表内条件。当控制器加入扩散模块时，利用条件独立性假设，有公式变化为：

\[ q(x*t\cdot|x*{t+1},x*c)\cdot=ZN(x_t;\mu*\theta(x*{t+1},t),\left(\sqrt{\frac{\beta_t(1-\bar{\alpha}\_t)}{1-\bar{\alpha}*{t+1}}}\right)^2)p(x_c|x_t) \]

其中，$q(x_t|x_{t+1},x_c)$是原始数据的逆向分布，学习的高斯模型$p_{\theta}(x_{t}| x_{t+1})$则简化为$p(x_c|x_t)$，$Z$是归一化常量。而在进一步推理过程中，参考文献将实例$x_c$的逆向分布近似为扰动高斯分布，使用取对数的方式得到下述公式：

\[ q(x*t\cdot|x*{t+1},x*c)\cdot=ZN(x_t;\mu*\theta(x*{t+1},t)+\sigma_t\cdot g_t,\left(\sqrt{\frac{\beta_t(1-\bar{\alpha}\_t)}{1-\bar{\alpha}*{t+1}}}\right)^2)p(x_c|x_t) \]

其中，$σ_t$是一个可学习的或预设的标量，用于控制调整的强度，而梯度$g_t=∇_(x_t ) Ctr1(x_t,c_i )$，这个梯度表示了为了满足条件$c_i$，数据$x_t$应该如何变化。然后对于条件$C$而言，参考文献基于编码后嵌入到联合分布空间的数据的两个元组如果高度相关，那么很可能在真实数据中共同出现的假设，使用余弦相似度作为控制器的相关性输出分数。因此，整个过程可以表达为下述公式：

\[ Ctrl(\mathrm{x}_c,\mathrm{x}_t,t)=CosineSimilarity\left(E_c(\mathrm{x}_c),E_R(\mathrm{x}_t,t)\right) \]

其中，$E_c$和$E_R$是两个编码器，$E_c$用于条件实例的元组，$E_R$用于要合成的表的元组，$t∈[0，T]$和$x_t$是从前向过程中采样的第$t$个噪声数据$q(x_t |x_0)$。

表格数据的预处理

考虑到表格数据的异质性，需要将表格数据统一为扩散模型可以接受的可逆模拟比特编码技术，将表格数据转换为扩散器可以处理的连续表示。下面给出模拟位编码面对表格数据的编码策略：

分类属性到序数整数的转换：对于分类属性$A_i$，从 0 开始分配序数，将数据转换为离散的数值属性。
序数整数到二进制位的转换：将每个 $A_i$ 的变量转换成二进制的向量，形式为 $\{0,1\}^d$，其中 $d = \log_2 |A_i|$
二进制位到实数的转换：接着把这些二进制位转换为实数，用于连续扩散模型
生成数据时的反转操作：通过阈值操作反转回二进制位，进而反转为对应分类属性。

实验

实验环境镜像: PyTorch 2.1.0，Python 3.10(ubuntu22.04)，Cuda 12.1 GPU: RTX 3090(24GB) * 1 CPU: 14 vCPU Intel(R) Xeon(R) Platinum 8362 CPU @ 2.80GHz
实验数据集在此采用参考文献配套的数据集，其中有三个单表和三个复表：
1. Default[5]包含有关信用卡客户的信息，包括人口统计因素、信用数据和付款违约状态。它是一个具有 30,000 个元组和 24 个属性的单个表。它通常用于预测客户是否会拖欠信用卡付款。数据集不平衡，多数类占 77.9%，少数类占 22.1%。
2. shoppers[6]关注在线购物者的行为，并包含有关他们的浏览和购买活动的信息。它是一个具有 12,330 个元组和 18 个属性的单个表。它经常被用来预测购物者的购买意图。数据集是不平衡的，多数类占元组的 84.5%，少数类占 15.5%。
3. WeatherAUS[7]是澳大利亚不同气象站跨越 10 年的每日天气观测的集合。我们关注的分类目标变量是“RainTomorrow”，它指示给定的一天是否下雨。数据集是不平衡的，多数(少数)类占元组的 78.0%(22.0%)。
4. heart[8]是一个心脏病数据库，其中包含两个表：Patient 和 Cardio。Patient 表包括患者信息，而 Cardio 表包含 8 个心电指数。这两个表可以使用 Patient ID 连接，连接的结果有 14 个属性和 200,000 个元组。
5. Airbnb[9]最初是从 Airbnb 数据库派生的住房信息的单一表格。我们遵循[27]将其正常化，以获得三个不同的表：房东表、邻居表和公寓表。这三个表的联接结果包含 26 个属性和 104,072 个元组
6. IMDB[10]是从流行的 IMDB 数据库派生出来的。我们将其标准化以获得五个表。具体来说，我们将关于电影的表合并得到 Movie 表，并将原始的 Person 表分为 Director 和 Actor，这两个表可以分别通过 Movie_Actor 和 Movie_Director 与 Movie 表连接。
实验评估指标表内数据增强：F1score 表间数据增强：bias_reduction：评估给定属性的真实完整数据分布能够被恢复得多好； re_reduction: 通过数据补全过程，查询结果的相对误差
模型参数

模块	参数	值
MLP 架构	隐藏层层数	4
	神经元	[512, 1024, 1024, 512]
	激活函数	ReLU
	Dropout	0.0
MLPBlock 参数	线性层	全连接层
	激活函数	ReLU
时间嵌入	SinTimeEmb 参数	正弦时间嵌入层
	激活函数	SiLU
控制器模块编码器	隐藏层层数	2
	神经元数量	[512, 512]
	激活函数	ReLU
	Dropout	0.0
训练参数	扩散模型学习率初始值	0.0018
	扩散模型学习率策略	线性学习率退火
	控制器学习率初始值	0.001
	控制器学习率策略	线性学习率退火
	扩散模型批量大小	4096
	控制器模型批量大小	512
	训练轮数	30000

实验结果

表 1 表内数据增强实验结果

数据集	处理方法	DT10	DT30	RF10	RF20	Adaboost	LR	MLP
Default	Identity	0.433	0.406	0.445	0.419	0.444	0.455	0.487
	RelDDPM	0.530	0.444	0.536	0.531	0.536	0.530	0.542
Shoppers	Identity	0.606	0.544	0.535	0.582	0.598	0.495	0.660
	RelDDPM	0.612	0.570	0.645	0.653	0.642	0.661	0.657
WeatherAUS	Identity	0.591	0.551	0.563	0.604	0.611	0.633	0.673
	RelDDPM	0.623	0.578	0.634	0.647	0.644	0.658	0.679

表 2 表间数据增强实验结果

数据集	bias_reduction	re_reduction
heart	0.213	0.799
imdb	0.053	0.545
Airbnb	0.302	0.508

从表 1 的结果可以看出，RelDDPM 在表内数据增强维度的效果较好，对下游分类模型的效果基本都有显著的提升。从表 2 中可以看出表间数据增强中，RelDDPM 模型在查询中错误减少的平均值方面保持较高的水准，也在保持原本数据分布方面保持的效果较优秀

参考文献

Vadim Borisov, Tobias Leemann, Kathrin Seßler, Johannes Haug, Martin Pawelczyk, and Gjergji Kasneci. Deep neural networks and tabular data: A survey. IEEE Transactions on Neural Networks and Learning Systems, 2022a.↩
Vadim Borisov, Kathrin Seßler, Tobias Leemann, Martin Pawelczyk, and Gjergji Kasneci. Language models are realistic tabular data generators. In The Eleventh International Conference on Learning Representations, ICLR 2023, Kigali, Rwanda, May 1-5, 2023. OpenReview.net, 2023a. URL https://openreview.net/pdf?id=cEygmQNOeI.↩